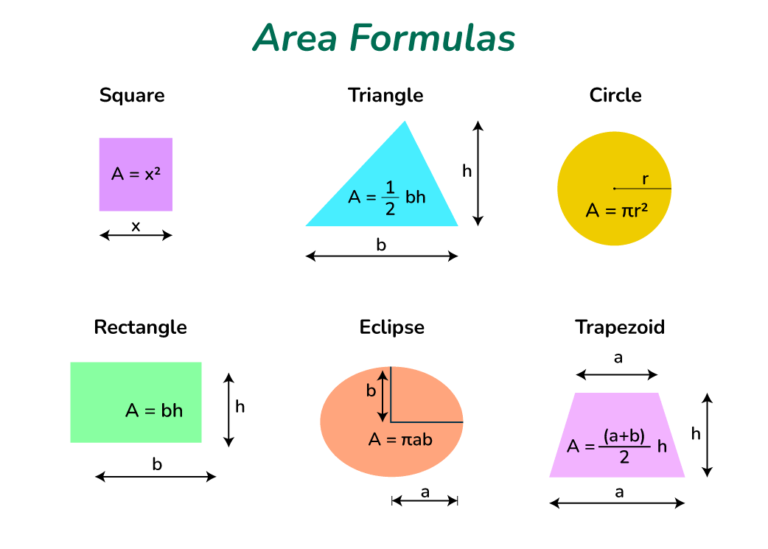
✅ L’aire se calcule avec des formules géométriques, du comptage de carreaux ou des intégrales pour des figures complexes; méthode selon la forme.
Le calcul de l’aire d’une surface est une opération fondamentale en mathématiques et en géométrie, utilisée pour déterminer l’étendue d’une figure plane. L’aire se mesure en unités carrées (cm2, m2, etc.) et sa méthode de calcul dépend de la forme de la figure concernée. Par exemple, l’aire d’un rectangle est obtenue en multipliant sa longueur par sa largeur, tandis que celle d’un triangle se calcule en prenant la moitié du produit de sa base par sa hauteur.
Nous allons explorer en détail les principales méthodes de calcul de l’aire selon les différentes figures géométriques classiques : rectangles, carrés, triangles, cercles, trapèzes, parallélogrammes, mais aussi des formes plus complexes comme les polygones réguliers ou irréguliers. Nous présenterons également des techniques comme la décomposition en figures simples, l’utilisation de coordonnées (avec la formule de Gauss pour les polygones), et aborderons le calcul d’aire par approximation pour les courbes et surfaces irrégulières. Enfin, des exemples pratiques et des conseils pour choisir la méthode adaptée selon le contexte vous seront fournis afin de vous permettre de maîtriser ces calculs essentiels.
Explication des Formules Spécifiques pour Différentes Figures Géométriques
L’aire représente la mesure de la surface occupée par une figure géométrique. Chaque forme a sa propre formule spécifique pour calculer cette surface, basée sur ses caractéristiques uniques. Comprendre ces formules est essentiel pour résoudre efficacement de nombreux problèmes en mathématiques, en architecture ou en ingénierie.
Calcul de l’aire du carré et du rectangle
Ces deux figures sont les plus simples et servent souvent d’introduction au calcul d’aires.
- Carré : Son aire est égale au carré de la longueur de son côté. La formule est A = c², où c est la longueur du côté.
- Rectangle : L’aire est obtenue en multipliant sa longueur par sa largeur. La formule est A = L × l, où L est la longueur et l la largeur.
Approche pour les triangles
Le triangle, figure aux trois côtés, utilise une formule bien connue :
A = (base × hauteur) / 2
Si la hauteur n’est pas connue, il est possible d’utiliser la formule de Héron :
A = √[s(s – a)(s – b)(s – c)], où a, b, c sont les côtés et s = (a + b + c)/2 est le demi-périmètre.
Les cercles : Calcul à partir du rayon
Le cercle se distingue par sa courbe continue et sa symétrie parfaite. Son aire se calcule grâce à la formule :
A = π × r²
avec r le rayon et π (approximativement 3,1416). Cette méthode est cruciale dans les applications liées à la physique et à la génie civil.
Illustration comparative des formules
| Figure Géométrique | Formule d’Aire | Variables |
|---|---|---|
| Carré | A = c² | c = côté |
| Rectangle | A = L × l | L = longueur, l = largeur |
| Triangle | A = (base × hauteur) / 2 ou A = √[s(s – a)(s – b)(s – c)] | base, hauteur ou a, b, c (côtés), s (demi-périmètre) |
| Cercle | A = π × r² | r = rayon |
Quelques cas et applications pratiques
Par exemple, dans le secteur de la construction, calculer l’aire d’un rectangle permet de déterminer la quantité de matériaux nécessaire, comme la peinture pour un mur. Pour les architectes, la formule du triangle est essentielle lorsqu’ils conçoivent des toits ou des plans urbains complexes.
De plus, en informatique graphique, le calcul de l’aire du cercle est crucial pour le rendu précis de formes circulaires dans des applications de modélisation 3D.
Conseils pratiques
- Vérifiez toujours les unités : L’aire est exprimée en unités carrées, par exemple centimètres carrés (cm²) ou mètres carrés (m²), et non en unités linéaires.
- Utilisez des formules adaptées : Ne pas hésiter à utiliser la formule de Héron pour les triangles lorsque la hauteur est difficile à mesurer.
- Maîtrisez les conversions : Selon les contextes, convertir les unités permet d’obtenir des résultats applicables et compréhensibles.
Questions fréquemment posées
Qu’est-ce que l’aire d’une surface ?
L’aire représente la mesure de la surface d’une figure en deux dimensions, souvent exprimée en unités carrées comme cm² ou m².
Quelles sont les méthodes standards pour calculer l’aire ?
Les méthodes principales sont la formule géométrique (longueur × largeur pour les rectangles), la décomposition en formes simples, et l’intégration pour les formes courbes.
Comment calcule-t-on l’aire d’un cercle ?
L’aire d’un cercle se calcule avec la formule A = π × r², où r est le rayon du cercle.
Peut-on calculer l’aire d’une forme irrégulière ?
Oui, on utilise souvent la méthode de subdivision en formes simples ou des outils numériques comme l’intégration ou la planimétrie.
Quelles unités sont utilisées pour mesurer l’aire ?
Les unités usuelles sont le mètre carré (m²), le centimètre carré (cm²), et parfois des unités plus grandes comme l’hectare.
Qu’est-ce que la méthode d’intégration pour le calcul d’aire ?
C’est une méthode utilisée en calcul avancé où l’aire sous une courbe est trouvée par intégration entre des bornes spécifiques.
| Méthode | Application | Formule / Technique | Exemple |
|---|---|---|---|
| Formules géométriques | Figures simples (rectangle, triangle, cercle) | Rectangle : L × l, Triangle : (base × hauteur)/2, Cercle : πr² | Rectangle 5×3 cm = 15 cm² |
| Décomposition en formes | Figures complexes divisibles en formes simples | Somme des aires des parties | Polygone divisé en triangles |
| Intégration | Formes courbes, fonctions mathématiques | ∫ y dx entre bornes a et b | Aire sous une courbe de f(x) |
| Planimétrie numérique | Calcul sur cartes, formes irrégulières | Logiciels utilisant des points et polygones | Calcul d’aires sur plan topographique |
N’hésitez pas à laisser vos commentaires ci-dessous et à consulter nos autres articles pour en savoir plus sur les mathématiques et la géométrie !